Restringiendo interfaces II: Modelando apariencias
Publicado por Miguel Viera el 19/02/2022
Refactoring, Interface Design, Design Patterns, Kotlin, DDD, Naming, Good Practices, SOLID, Types, Interfaces
Volvemos con la segunda parte de Restringiendo Interfaces. En esta ocasión hablaremos de cómo heredar modelos existentes puede adulterar su diseño, provocando la ilusión de que es la forma más fiel de modelar el dominio del problema. En este post veremos que, para implementar diseños más fieles al problema, debemos cuidar el proceso de creación de interfaces, y evitar dejarnos embaucar por modelos heredados que podrían limitar nuestra visión..
Para plantear esta idea, usaremos un problema sencillo, estudiando, en primer lugar, un posible modelado que presenta los problemas de diseño que queremos evitar. A continuación, comentaremos un modelado alternativo que mejora el enfoque inicial resolviendo sus problemas. Modelaremos el recuento de puntos de un partido de tenis, pero centrándonos sólo en el subproblema de conseguir un punto de set. Partiremos de la siguiente definición:

Un marcador de tenis se compone de sets, puntos de set, y puntos de juegos. Para ganar un punto de set, hay que jugar varios puntos de juego. Los jugadores parten de 0-0, cuando un jugador gana un punto se suma 15 al marcador, por ejemplo, 0-15. Una vez llegas a 30, suman 10, es decir, 0-40, y si ese jugador gana el siguiente punto, ganaría el punto de set. En el caso de empatar en 40-40 (denominado Deuce), se procede a conceder ventajas de juego, por ejemplo Ad.-40. Si el jugador que va por detrás marca otro punto de juego, el marcador regresa a Deuce, y se volvería a repetir que si algún jugador gana el siguiente punto de juego, se concede una ventaja. Para ganar el punto de set, se necesita ganar un punto cuando tienes una ventaja, o lo que es lo mismo, se gana con una diferencia de dos puntos por encima del otro jugador.
Una progresión del marcador de un set válida sería la siguiente:
0-0 -> 0-15 -> 15-15 -> 15-30 -> 30-30 -> 40-30 -> 40-40 -> Ad.-40
Con esta descripción podríamos empezar a modelar. Como dijimos partiremos de una implementación factible y la iremos transformando poco a poco para exponer las ideas que pretendo explorar en este post. La implementación inicial pertenece a enunciado de la Kata de refactoring Tennis.
| class TennisGame { | |
| private var mScore1: Int = 0 | |
| private var mScore2: Int = 0 | |
| override fun wonPoint(playerName: String) { | |
| if (playerName === "player1") mScore1 += 1 | |
| else mScore2 += 1 | |
| } | |
| override fun getScore(): String { | |
| var tempScore = 0 | |
| if (mScore1 == mScore2) { | |
| return when (mScore1) { | |
| 0 -> score = "Love-All" | |
| 1 -> score = "Fifteen-All" | |
| 2 -> score = "Thirty-All" | |
| else -> score = "Deuce" | |
| } | |
| } else if (mScore1 >= 4 || mScore2 >= 4) { | |
| val minusResult = mScore1 - mScore2 | |
| if (minusResult == 1) return "Advantage player1" | |
| else if (minusResult == -1) return "Advantage player2" | |
| else if (minusResult >= 2) return "Win for player1" | |
| else return "Win for player2" | |
| } else { | |
| var score = "" | |
| for (i in 1..2) { | |
| if (i == 1) | |
| tempScore = mScore1 | |
| else { | |
| score += "-" | |
| tempScore = mScore2 | |
| } | |
| when (tempScore) { | |
| 0 -> score += "Love" | |
| 1 -> score += "Fifteen" | |
| 2 -> score += "Thirty" | |
| 3 -> score += "Forty" | |
| } | |
| } | |
| } | |
| return score | |
| } | |
| } |
Lo que hace este código es llamar al método wonPoint(playerName) con el nombre del jugador (o equipo) que marca
el punto y sumarle un punto en el marcador. Luego, el cliente que consume este código, llama al método getScore() que devuelve la puntuación
con un tipo String que representa los puntos de juego en la jerga del tenis.
A partir de este código podemos analizar qué heurísticas podrían haber llevado a esta implementación. Lo primero que observamos
es que para determinar los puntos de un jugador, se emplean operaciones aritméticas, es decir, cada vez que un jugador gana un punto,se almacena el estado en los campos mScore1 o mScore2. Además, los valores numéricos empleados para operar con los puntos no son los
mismos que se emplean para representar los puntos de juego de un set, en su lugar, se usa una serie matemática infinita
de números enteros para calcular la puntuación del jugador.
Estamos ante un problema típico de implementación, como el que vimos
en el post anterior: existe un Connascence of Meaning, es decir, hay valores en el código que tienen un significado implícito no reflejado en el diseño. Este problema de diseño también lo podríamos haber identificaco mediante otra heurística: los Code Smells. En este caso estaríamos ante un Data Clump. Los Data Clumps hacen referencia a aquellos datos datos que sólo tienen sentido cuando están juntos, y que de forma implícita se relacionan. Si uno de esos datos cambia, el otro se ve forzado a cambiar conjuntamente. Este ejemplo lo podemos encontrar en la representación de la serie aritmética en los campos mScore1 y mScore2y el método getScore(), ambos datos se interrelacionan, pues score necesita conocer la lógica de la progresión de la serie para poder operar con ella y saber cuál es el valor de marcador que tiene que devolver y la serie conoce como getScore() emplea sus datos para poder identificar el marcador y por tanto, no puede cambiar libremente. Podríamos suavizar este problema de diseño de forma implícita si los números que empleamos en estas operaciones aritméticas fuesen los mismos que usa el problema en su definición (0, 15, 30, 40). Pero nuestro diseño seguiría sin utilizar tipos complejos para representar y forzar que sólo podamos elegir valores correctos, ya que la interfaz actual no restringe qué valores se pueden usar. La definición implícita que generaríamos sólo sería válida si el desarrollador
conoce bien las reglas del tenis, en caso contrario, estaríamos en la casilla de salida, es decir, la solución de limitar los números utilizados en las operaciones aritméticas, no ayudaría a hacer más explícitas las reglas de negocio ni adocumentar el comportamiento del código para facilitar su comprensión.
El problema que presenta el al método getScore() se debe a que la elección de representar
los puntos como un entero que sigue una serie en incrementos de uno, fuerza a mantenerlos puntos como estado local para poder determinar el momento del juego en el que se está (es decir, los marcadores entre el 0-0 y Deuce, Advantage y Victoria) y saber si hay algún jugador que va por delante, hay empate o se ha ganado el punto de set. El hecho de que cuando un jugador gana un punto de juego se incremente la serie, obliga a que el método getScore() tenga que absorber el comportamiento del cálculo de puntos y que no tenga exclusivamente su representación.
Este diseño tiene por tanto dos problemas pronunciados:
- Representar los posibles estados del problema con números ajenos a su definición. Esto ha complicado el algoritmo que permite obtener los puntos actuales de ambos jugadores agravando el Connascence of Meaning. Los posibles valores de la serie implican que el mismo valor puede significar diferentes cosas según el estado que se encuentre el marcador y a medida que se altere. Lo que nos lleva al segundo problema.
- La identidad del mismo valor cambia y puede tener un significado distinto, y su ”Meaning”, se superpone a la serie matemática. Este tipo de acoplamiento se denomina Connascence of Algorithm, que implica que varias partes de nuestro diseño conocen la lógica interna del algoritmo e implícitamente aceptan un contrato sobre la transformación de los datos. Este problema lo encontramos a medida que avance la serie a medida que transcurre el partido. Por ejemplo, pongamos que los jugadores van 40-40 (Deuce), el estado de nuestra clase la primera vez que llegan a esta puntuación es de 3-3. Pero hay diferentes estados de nuestra serie que significan también empate, como por ejemplo: 4-4, 5-5, 99-99… Pero en un marcador de 4-2, el cuatro significa victoria, mientras que en un 4-3, significa ventaja. Por tanto, el mismo valor puede significar hasta cuatro cosas distintas.
Implementando el rediseño
El primer paso y el más barato, en términos de economía de software, es eliminar el tipo String del playerName y lo sustituimos por un tipo enumerado que represente
a los dos posibles jugadores (o equipos) que pueden jugar un partido de tenis, eliminando así el Connascence of Meaning del player y a su vez protegiéndonos con el compilador de posibles entradas no válidas.
Luego para resolver el problema de la serie emplearemos sólo el rango de valores posibles para los puntos de juego de un partido de tenis.
Este sería el resultado de nuestra primera transformación:
| public enum Player { | |
| PLAYER_1, | |
| PLAYER_2 | |
| } | |
| ... | |
| override fun wonPoint(player: Player) { | |
| if (player == Player.PLAYER_1) | |
| when (mScore1) { | |
| 0 -> mScore1 += 15 | |
| 15 -> mScore1 += 15 | |
| 30 -> mScore1 += 10 | |
| 40 -> { | |
| when (mScore2) { | |
| 40 -> mScore1 = 41 | |
| 41 -> { | |
| mScore1 = 40 | |
| mScore2 = 40 | |
| } | |
| else -> mScore1 = 50 | |
| } | |
| } | |
| } | |
| else | |
| when (mScore2) { | |
| 0 -> mScore2 += 15 | |
| 15 -> mScore2 += 15 | |
| 30 -> mScore2 += 10 | |
| 40 -> { | |
| when (mScore1) { | |
| 40 -> mScore2 = 41 | |
| 41 -> { | |
| mScore1 = 40 | |
| mScore2 = 40 | |
| } | |
| else -> mScore2 = 50 | |
| } | |
| } | |
| } | |
| } | |
| override fun getScore(): String { | |
| if (mScore1 == mScore2) { | |
| return when (mScore1) { | |
| 0 -> "Love-All" | |
| 15 -> "Fifteen-All" | |
| 30-> "Thirty-All" | |
| else -> "Deuce" | |
| } | |
| } | |
| if (mScore1 >= 40 || mScore2 >= 40) { | |
| return if (mScore1 == 41) | |
| "Advantage player1" | |
| else if (mScore2 == 41) | |
| "Advantage player2" | |
| else if (mScore1 == 50) | |
| "Win for player1" | |
| else | |
| "Win for player2" | |
| } | |
| val player1 = when (mScore1) { | |
| 0 -> "Love" | |
| 15 -> "Fifteen" | |
| 30 -> "Thirty" | |
| 40 -> "Forty" | |
| else -> throw Exception("Invalid value") | |
| } | |
| val player2 = when (mScore2) { | |
| 0 -> "Love" | |
| 15 -> "Fifteen" | |
| 30 -> "Thirty" | |
| 40 -> "Forty" | |
| else -> throw Exception("Invalid value") | |
| } | |
| return "$player1-$player2" | |
| } | |
| ... |
El siguiente paso es reducir la complejidad ciclomática en el método
getScore() que calculaba la representación de los puntos de los jugadores. Para conseguirlo, primero, duplicamos el código del for que contiene.
Y a continuación, hacemos que sólo emplee los valores de los puntos posibles en un juego de tenis mediante un switch.
Con esto llevamos la lógica del cálculo aritmético al método wonPoint(Player), que ahora es capaz de reflejar, usando estos valores, cómo funciona
un marcador, consiguiendo así centralizar en un único lugar esa responsabilidad En el proceso hemos inventado dos nuevos valores que no pueden soportar una de las lógicas del problema, la ventaja de un jugador y la victoria. Esto se debe a que tanto la ventaja de un jugador como la victoria en el punto
de set no tienen valores numéricos asociados. Los valores elegidos para representar estos últimos son el 41, para la ventaja de algunos de los jugadores y el 50, para la victoria.
El porqué de esta última decisión la podemos entender como un paso intermedio en el refactor. Ahora mismo en el proceso de descubrir nuestro diseño optamos por elegir valores ajenos a la definición del problema para que generen ruido y la necesidad de eliminarlos al final.
Con este refactor hemos obtenido nuevos aprendizajes sobre el problema:
- Los valores de victoria y ventaja no son numéricos, son estados que se representan de forma distinta al resto del conjunto de valores numéricos posibles. La nueva implementación que elimina la serie matemática que almacenaba el estado y que se usaba para calcular quién iba ganando, nos desvela otra perspectiva sobre el diseño. Gracias al marcador de ventaja y la victoria, podemos exponer esta nueva interpretación, en un Deuce el jugador que gane el siguiente punto y adquiera ventaja (40-Ad.), sólo tiene dos posibles estados siguientes, volver al Deuce o ganar el punto. Además otro detalle que podemos observar es que existen diferentes combinaciones de puntos desde las que podemos alcanzar la victoria de algún jugador.
- Podemos deducir que estamos ante a una máquina de estados finita, lo cual nos permitiría replantear el algoritmo desde otra perspectiva. Si representamos los puntos como transiciones de estado sobre un diagrama de estados tendríamos algo tal que así:
Marcador como máquina de estados
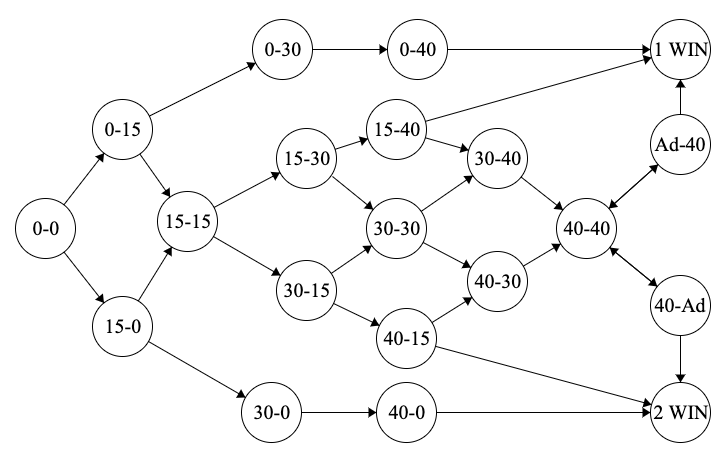
Tenemos 20 posibles estados dentro de nuestro problema, algo bastante sencillo de modelar y que nos permitiría eliminar las operaciones aritméticas de nuestro código. Representar los puntos mediante valores numéricos nos impedía ver otras opciones de diseño más sencillas con las que plantear el problema y limitar el dominio de posibles valores.
Marcador como máquina de estados simplificada
Podemos también emplear una simplificación de la máquina de estados a través de un transductor de estados como la máquina de Mealy y a partir de las entradas identificar estados que son comunes y que representan a un único estado duplicado múltiples veces. En este caso podemos reducir los 20 estados a un total de 4, Initial, para los valores comprendidos entre el 0-0 y el 40-40, Deuce, para 40-40, Advantage para los marcadores 40-Ad. y Ad.-40 y Win, para cuando un jugador gana la partida, quedando de esta manera:
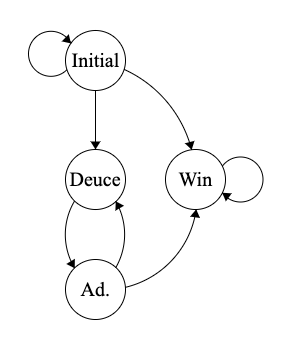
Un detalle importante es entender que hay múltiples procesos para alcanzar esta solución. En el caso que nos atañe, lo hemos conseguido a través del análisis del estado a partir de los posibles valores del tenis. Pero si hubiéramos partido del análisis del comportamiento en vez de enfocarnos en los valores, hubiéramos llegado al mismo sitio. El State Pattern que vamos a emplear para diseñar la nueva solución permite desde el análisis del problema, encontrar el patrón en el problema por las fuerzas y motivaciones detrás del mismo. No es necesaria usar la fuerza bruta para conseguir llegar a la solución que ahora veremos, en este caso he querido que sea así por analizar este caso que me parece curioso, pero es importante no confundir State Pattern = Máquina de estados finita.
Luego de este análisis, podemos empezar a transformar el código utilizando el State Pattern. Este patrón nos ayudará a representar los diferentes estados de las máquinas que hemos diseñado a partir del código anterior. También tiene un valor añadido porque solventará el Data Clump del getScore() y y mScore1 y mScore2 en los nuevos objetos que representan el estado. Pero lo más importante es que cada lógica de transición de un estado a otro estará albergada dentro de la lógica de las diferentes clases que surjan en la implementación.
| enum class Scoreboard( | |
| val player1NextScore: () -> Scoreboard, | |
| val player2NextScore: () -> Scoreboard, | |
| val score: String | |
| ) { | |
| ZERO_ZERO({ FIFTEEN_ZERO }, { ZERO_FIFTEEN }, "Love-All"), | |
| ZERO_FIFTEEN({ FIFTEEN_FIFTEEN }, { ZERO_THIRTY }, "Love-Fifteen"), | |
| ZERO_THIRTY({ FIFTEEN_THIRTY }, { ZERO_FORTY }, "Love-Thirty"), | |
| ZERO_FORTY({ FIFTEEN_FORTY }, { PLAYER_TWO_WIN }, "Love-Forty"), | |
| FIFTEEN_ZERO({ THIRTY_ZERO }, { FIFTEEN_FIFTEEN }, "Fifteen-Love"), | |
| THIRTY_ZERO({ FORTY_ZERO }, { THIRTY_FIFTEEN }, "Thirty-Love"), | |
| FORTY_ZERO({ PLAYER_ONE_WIN }, { FORTY_FIFTEEN }, "Forty-Love"), | |
| FIFTEEN_FIFTEEN({ THIRTY_FIFTEEN }, { FIFTEEN_THIRTY }, "Fifteen-All"), | |
| FIFTEEN_THIRTY({ THIRTY_THIRTY }, { FIFTEEN_FORTY }, "Fifteen-Thirty"), | |
| FIFTEEN_FORTY({ THIRTY_FORTY }, { PLAYER_TWO_WIN }, "Fifteen-Forty"), | |
| THIRTY_FIFTEEN({ FORTY_FIFTEEN }, { THIRTY_THIRTY }, "Thirty-Fifteen"), | |
| THIRTY_THIRTY({ FORTY_THIRTY }, { THIRTY_FORTY }, "Thirty-All"), | |
| THIRTY_FORTY({ FORTY_FORTY }, { PLAYER_TWO_WIN },"Thirty-Forty"), | |
| FORTY_FIFTEEN({ PLAYER_ONE_WIN }, { FORTY_THIRTY }, "Forty-Fifteen"), | |
| FORTY_THIRTY({ PLAYER_ONE_WIN }, { FORTY_FORTY }, "Forty-Thirty"), | |
| FORTY_FORTY({ ADVANTAGE_FORTY }, { FORTY_ADVANTAGE }, "Deuce"), | |
| ADVANTAGE_FORTY({ PLAYER_ONE_WIN }, { FORTY_FORTY },"Advantage player1"), | |
| FORTY_ADVANTAGE({ FORTY_FORTY }, { PLAYER_TWO_WIN }, "Advantage player2"), | |
| PLAYER_ONE_WIN({ PLAYER_ONE_WIN }, { PLAYER_ONE_WIN }, "Win for player1"), | |
| PLAYER_TWO_WIN({ PLAYER_TWO_WIN }, { PLAYER_TWO_WIN}, "Win for player2"); | |
| } | |
| class TennisGame { | |
| private var points = Scoreboard.ZERO_ZERO | |
| fun wonPoint(player: Player) { | |
| points = when (player) { | |
| PLAYER_1 -> points.player1NextScore() | |
| PLAYER_2 -> points.player2NextScore() | |
| } | |
| } | |
| fun getScore() = points.score | |
| } |
Este código es el que representa la primera máquina de estados. Esta sería la propuesta inicial de la implementación. Hemos eliminado las operaciones aritméticas y hemos creado el conjunto de transiciones de estados posibles a través de una nueva clase Scoreboard que aglomera la puntuación actual de ambos jugadores y cuando alguno de los dos marca un nuevo punto de juego, se transiciona a otro estado que refleje la victoria de ese jugador. Esta nueva clase absorbe ambos switch de TennisGame y se reemplazan a través del refactor Replace conditional with Polymorphism que lo elimina de los método wonPoint(Player) y getScore().
Si ahora eliminamos la duplicación de estados que hemos dicho anteriormente y representamos la máquina de estados simplificada el resultado será el siguiente:
| class TennisGame { | |
| private var score : Scoreboard = Initial.new() | |
| fun wonPoint(player: Player) { | |
| score = when (player) { | |
| PLAYER_1 -> score.player1NextScore() | |
| PLAYER_2 -> score.player2NextScore() | |
| } | |
| } | |
| fun getScore() = score.score() | |
| } | |
| interface Scoreboard { | |
| fun player1NextScore(): Scoreboard | |
| fun player2NextScore(): Scoreboard | |
| fun score(): String | |
| } | |
| class Initial private constructor(private var player1Points: GamePoints, private var player2Points: GamePoints) : Scoreboard { | |
| companion object { | |
| fun new() : Scoreboard = Initial(LOVE, LOVE) | |
| } | |
| override fun player1NextScore(): Scoreboard = when (player1Points) { | |
| LOVE, FIFTEEN -> Initial(player1Points.next(), player2Points) | |
| THIRTY -> if (player2Points == FORTY) Deuce() else Initial(player1Points.next(), player2Points) | |
| FORTY -> Win(PLAYER_1) | |
| } | |
| override fun player2NextScore(): Scoreboard = when (player2Points) { | |
| LOVE, FIFTEEN -> Initial(player1Points, player2Points.next()) | |
| THIRTY -> if (player1Points == FORTY) Deuce() else Initial(player1Points, player2Points.next()) | |
| FORTY -> Win(PLAYER_2) | |
| } | |
| override fun score(): String = | |
| if (player1Points == player2Points) "${player1Points.displayName}-All" | |
| else "${player1Points.displayName}-${player2Points.displayName}" | |
| private enum class GamePoints(val displayName: String, val next: () -> GamePoints) { | |
| LOVE("Love", { FIFTEEN }), | |
| FIFTEEN("Fifteen", { THIRTY }), | |
| THIRTY("Thirty", { FORTY }), | |
| FORTY("Forty", { FORTY }) | |
| } | |
| } | |
| class Deuce : Scoreboard { | |
| override fun player1NextScore(): Scoreboard = Advantage(PLAYER_1) | |
| override fun player2NextScore(): Scoreboard = Advantage(PLAYER_2) | |
| override fun score(): String = "Deuce" | |
| } | |
| class Advantage(private val advantagedPlayer: Player) : Scoreboard { | |
| override fun player1NextScore(): Scoreboard = when (advantagedPlayer) { | |
| PLAYER_1 -> Win(advantagedPlayer) | |
| PLAYER_2 -> Deuce() | |
| } | |
| override fun player2NextScore(): Scoreboard = when (advantagedPlayer) { | |
| PLAYER_1 -> Deuce() | |
| PLAYER_2 -> Win(advantagedPlayer) | |
| } | |
| override fun score(): String = when (advantagedPlayer) { | |
| PLAYER_1 -> "Advantage player1" | |
| PLAYER_2 -> "Advantage player2" | |
| } | |
| } | |
| class Win(private val winner: Player) : Scoreboard { | |
| override fun player1NextScore(): Scoreboard = Win(winner) | |
| override fun player2NextScore(): Scoreboard = Win(winner) | |
| override fun score() : String = when (winner) { | |
| PLAYER_1 -> "Win for player1" | |
| PLAYER_2 -> "Win for player2" | |
| } | |
| } |
Como se puede observar, la clase ScoreBoard se convierte en interfaz y deja de ser un enumerado, y tenemos diferentes implementaciones de la interfaz en las clases Initial, Deuce, Advantage y Win. Initial absorbe la lógica de transición entre los estados duplicados y es la que avanza de estado una vez se llega a 40-40, que transiciona al estado Deuce. Deuce concederá ventajas avanzando al estado Advantage y este último avanza a Win si un jugador ganó o volverá a Deuce si vuelven a empatar.
Ambos diseños son inmutables, las transiciones entre estados no producen cambio interno de estado. En la primera implementación al ser un enumerado es bastante fácil de ver pues es un enumerado sin estado interno. Pero en el caso de la implementación de la máquina de estados simplificada hay que observar que aunque Initial, alberga estado, no lo modifica internamente, lo que hace es crear un estado nuevo a partir de su propio estado modificado, que puede ser mantenerse en el estado actual o transicionar a otro estado con estos nuevos valores.
Conclusiones
Como comenté en el post anterior, la clave de diseñar interfaces no trata sólo de definir interfaces a prueba de errores humanos, sino también hacerlas semánticas. Esto lo hemos visto con ambas implementaciones, pues ambas son restrictivas y semánticas.
En el caso de la Initial, Deuce, Advantage y Win, hemos creado un nuevo término no existente en la jerga para expresar un abstracción subyacente en el modelo, mientras que la otra si que es fiel a la jerga existente. Ambas opciones son perfectamente válidas y a la hora de elegir el diseño final es tener claros los ejes de cambio [1] [2] de nuestro sistema. En el caso del tenis es sencillo, al ser un problema acotado y definido, podríamos quedarnos con la solución con 20 estados aunque su dominio sea espacialmente mayor por la duplicidad del mismo estado varias veces. La solución de cuatro estados coloca en un sitio más cohesivo la lógica de a qué estado tiene que avanzar. Ante un problema que no fuera de dominio finito preferiría la solución con menos estados ya que su diseño es más fácil evolucionar para satisfacer nuevas necesidades de negocio. Así que, aquí te dejo elegir la solución que más consideres oportuna para la Kata Tennis, elige tus tradeoffs y como dice Richard Hickey “Pick your poison”.
Es muy valioso que al diseñar intentamos siempre evaluar desde múltiples heurísticas los problemas que podemos encontrar en nuestros diseños. En esta kata concretamente, esta práctica nos ha aportado mucho porque identificar los diferentes tipos de Connascence (Meaning y Algorithm), el code smell Data Clump y ver que las fuerzas del problema se corresponden con las del patrón estado ha empujado a nuestro diseño al mismo destino gracias a triangular los mismos síntomas desde diferentes perspectivas o heurísticas. Lo interesante es que en este caso el resultado de aplicar las diferentes heurísticas se reforzaban unas a otras ya que se apuntaban a la misma dirección de diseño.
Cuando empezamos a definir el ejemplo del juego de tenis encontramos varios elementos que definen el lenguaje del espacio del problema, y surgen valores o elementos que representan el dominio del mismo. Cuando se nos da un código como el inicial, que toma ciertas decisiones de diseño que resuelven el problema obviando este lenguaje/elementos/dominio,** nos alejamos de encontrar una solución que sea más semántica con el problema y dejamos permear en el diseño detalles de bajo nivel que distraen a quien lo lee.** Emplear únicamente la serie aritmética infinita dejaba exponer un diseño más acorde al tipo de problema que presenta la kata tenis y la primera transformación que hicimos fue seguir asumiendo que el problema era exclusivamente matemático, pues la solución ya lo contemplaba, y los valores posibles dentro del enunciado, a excepción de la ventaja y victoria, eran numéricos. Cuando modelamos un problema es necesario mirarlo o tratar de representarlo desde varios prismas, para evitar caer en la trampa de la solución aparente. No hay que caer en la trampa de elegir la opción más sencilla de percibir, pero que representa el problema con un diseño más complejo, que escoger la opción menos aparente, pero que más se adapta al problema. Pensar en los límites de tus valores de entrada puede ser una heurística que te ayude a acotar el problema y guiarte a modelar tus interfaces correctamente y seguir destilando el problema hasta dar con el diseño que buscas. Además es útil conocer y aplicar otras heurísticas, como el connascence, los code smells o los patrones, para contrastar el diseño que vas encontrando.
Espero que te haya gustado el post y que me des feedback de qué te ha parecido.
Referencias:
- Refactoring, Martin Fowler. Mencionados en el post:
Refactoring to Polymorphism y Data Clump. - Design Patterns: Elements of Reusable Object-Oriented Software, Erich Gamma, Ralph Johnson, John Vlissides, Richard Helm. El mencionado en el post
State Pattern. - About Connascence, Manuel Rivero.
- Examples lists in TDD, Manuel Rivero.
- Single Responsibility ¿Principle?, The Big Branch Theory podcasts.
- Code Smells, Martin Fowler.
- Data clumps, primitive obsession and hidden tuples, Manuel Rivero.
- Refactoring Kata Tennis to State Pattern, Manuel Rivero.